Tutorial on Frequency Control and Timing Application of Quartz Crystal Resonators and Oscillators (Part 3)

Zero Temperature Coefficient Quartz Cuts

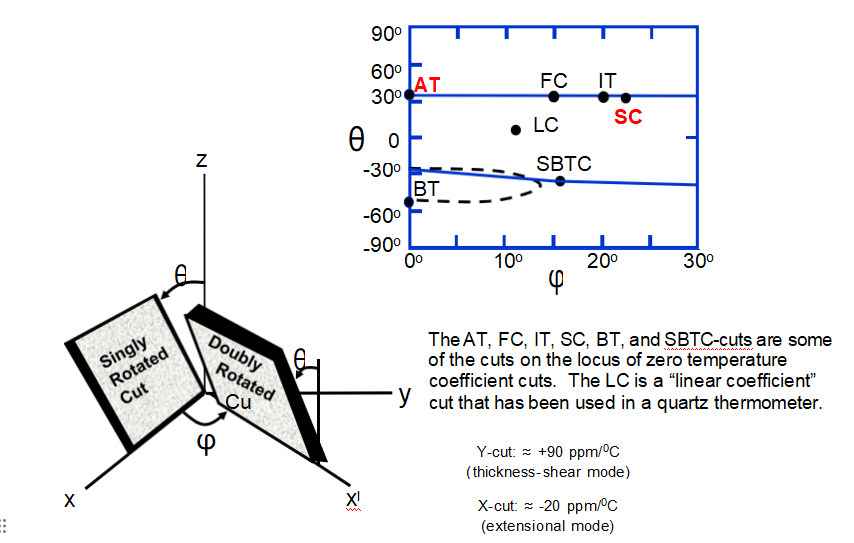
Comparison of SC and AT-cuts

•  Advantages of the SC- cut

•  Thermal transient compensated (allows faster warmup OCXO)

•  Static and dynamic f vs. T allow higher stability OCXO and MCXO

•  Better f vs. T repeatability allows higher stability OCXO and MCXO

•  Far fewer activity dips

•  Lower drive level sensitivity

•  Planar stress compensated; lower Δf due to edge forces and bending

•  Lower sensitivity to radiation

•  Higher capacitance ratio (less Δf for oscillator reactance changes)

•  Higher Q for fundamental mode resonators of similar geometry

•  Less sensitive to plate geometry - can use wide range of contours

•   Disadvantage of the SC-cut   :  More difficult to manufacture for OCXO (but  is easier to manufacture for MCXO than is an AT-cut for precision TCXO)

 

•   Other Significant Differences

•  B-mode is excited in the SC-cut, although not necessarily in LFR's

•  The  SC-cut is sensitive to electric fields (which can be used for compensation)

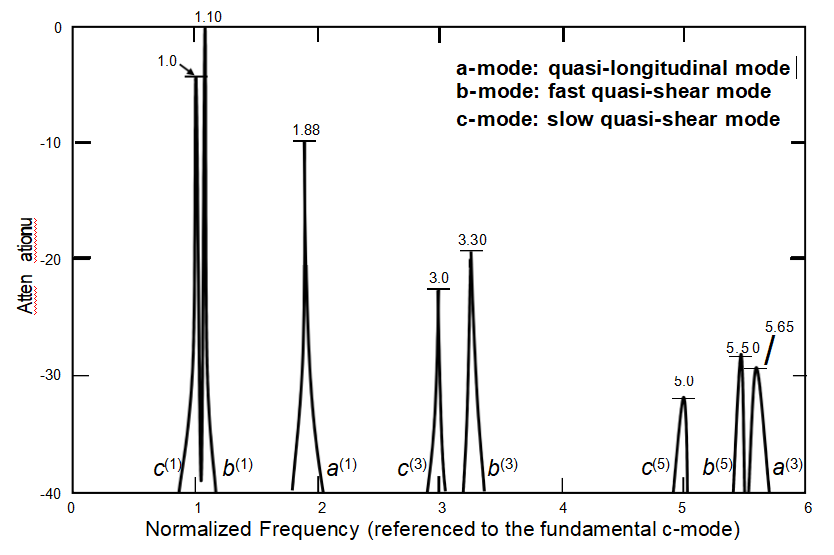
Mode Spectrograph of an SC-cut

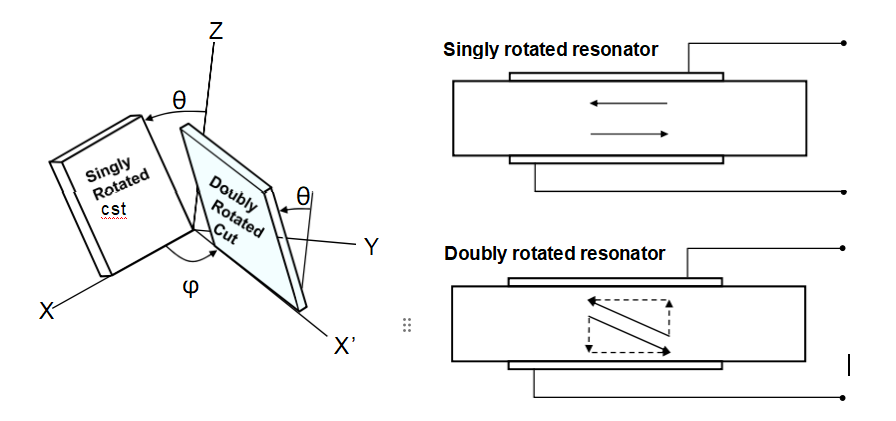
Singly Rotated and Doubly Rotated Cuts’ Vibrational Displacements

Resonator Packaging

Two-point Mount Package           Three- and Four-point Mount Package

Equivalent Circuits

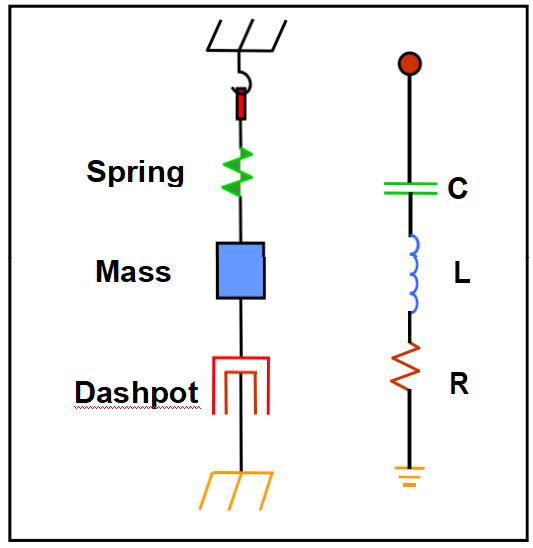
Equivalent Circuit of a Resonator

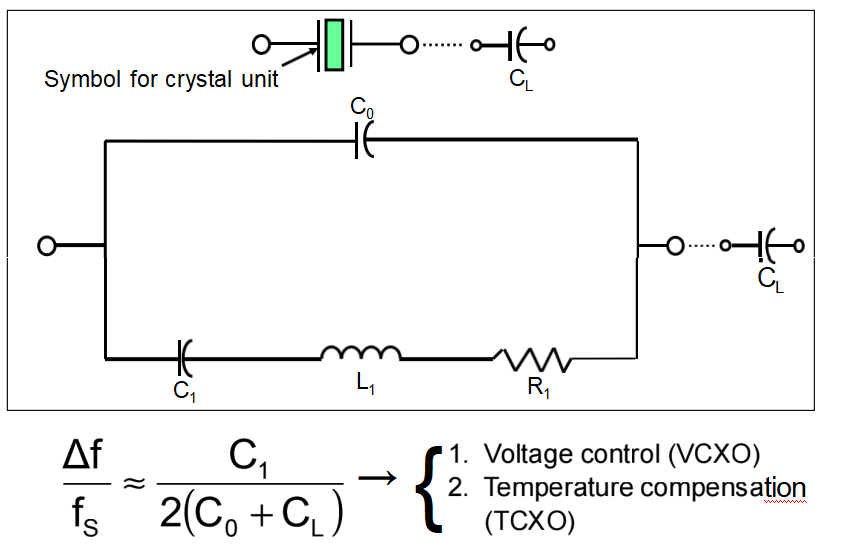
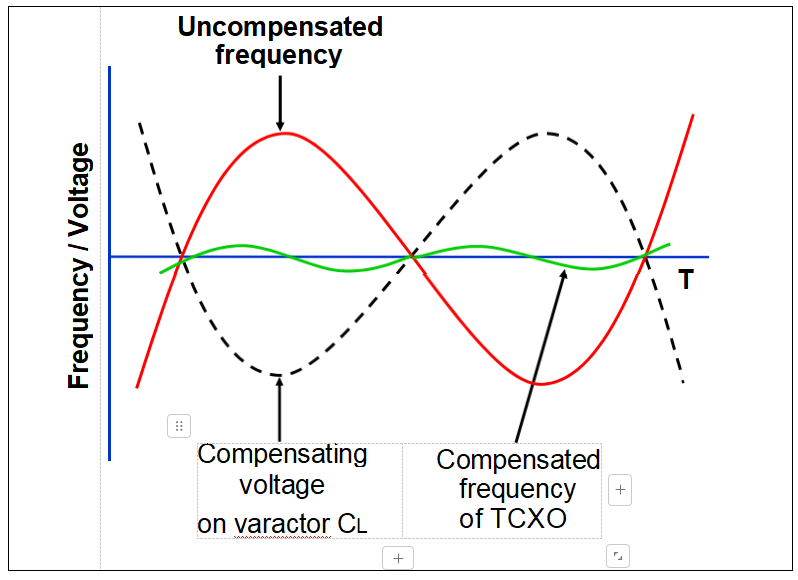
Crystal Oscillator f vs. T Compensation

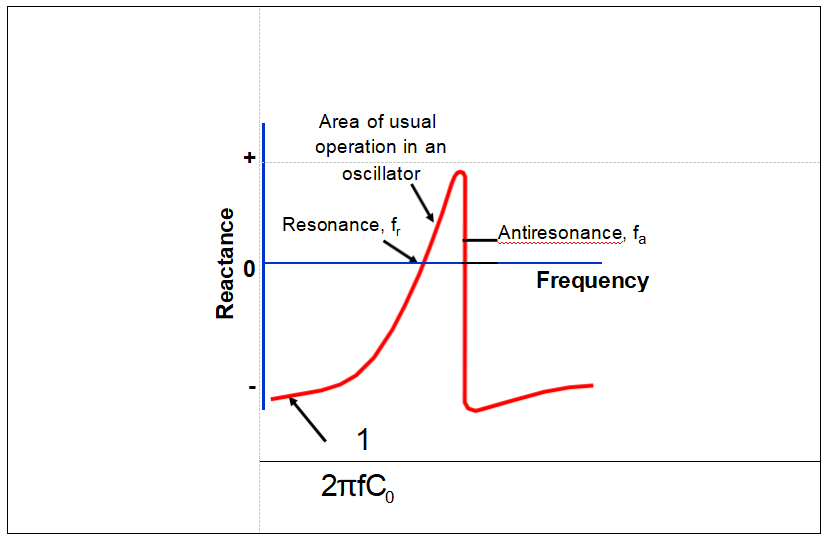
Resonator Reactance vs. Frequency

Equivalent Circuit Parameter Relationships

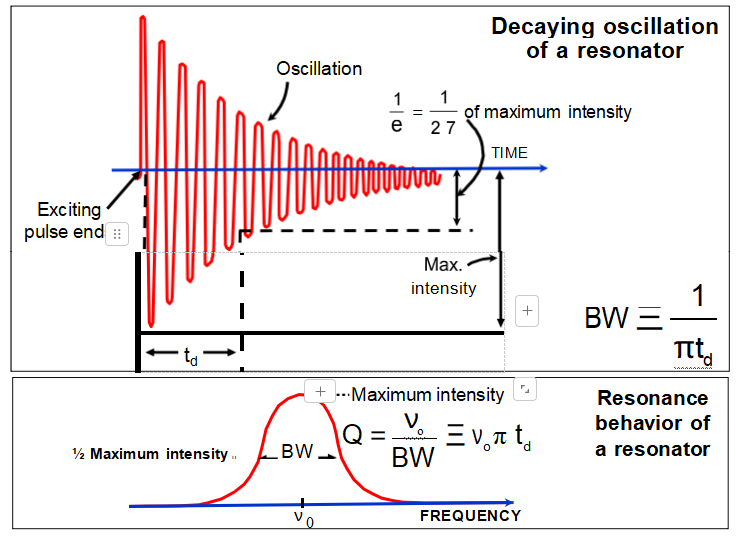
                                               What is Q and Why is it Important?

Q is proportional to the decay-time, and is inversely

proportional to the linewidth of resonance (see next page).

• The higher the Q, the higher the frequency stability and accuracy capability  of a resonator (i.e., high Q is a

necessary but not a sufficient condition).  If, e.g., Q = 106 ,    then 10-10 accuracy requires ability to determine center of    resonance curve to 0.01% of the linewidth, and stability (for some averaging time) of 10-12  requires ability to stay near    peak of resonance curve to 10-6  of linewidth.

 

•   Phase noise close to the carrier has an especially strong dependence on Q ( 上(f) ∝ 1/Q4 for quartz oscillators).

Decay Time, Linewidth, and Q

Factors that Determine Resonator Q

The  maximum   Q  of a resonator can be expressed as:

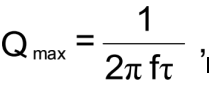
where f is the frequency in Hz, and τ is an empirically determined “motional

time constant” in seconds, which varies with the angles of cut and the mode    of vibration.  For example, τ = 1 x 10-14s for the AT-cut's c-mode (Q max  = 3.2     million at 5 MHz), τ = 9.9 x 10 -15s for the SC-cut's c-mode, and τ = 4.9 x 10 -15s for the BT-cut's b-mode.

Other   factors  which affect the Q of a resonator include:

 

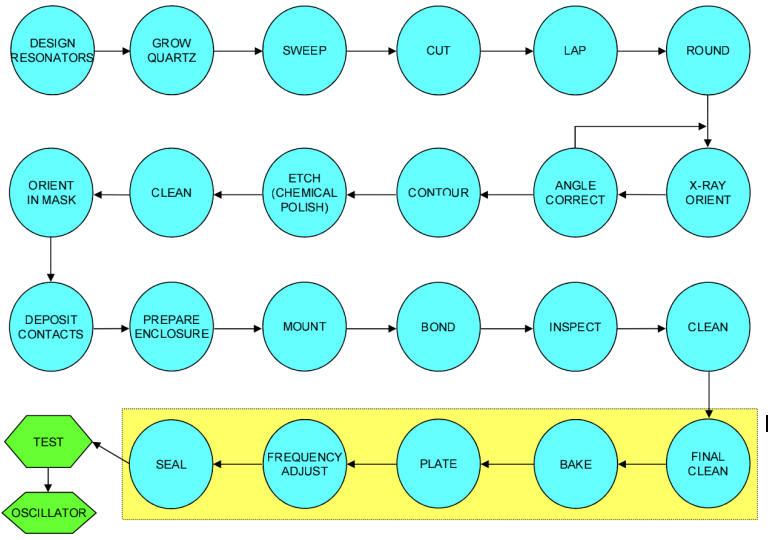
Resonator Fabrication Steps

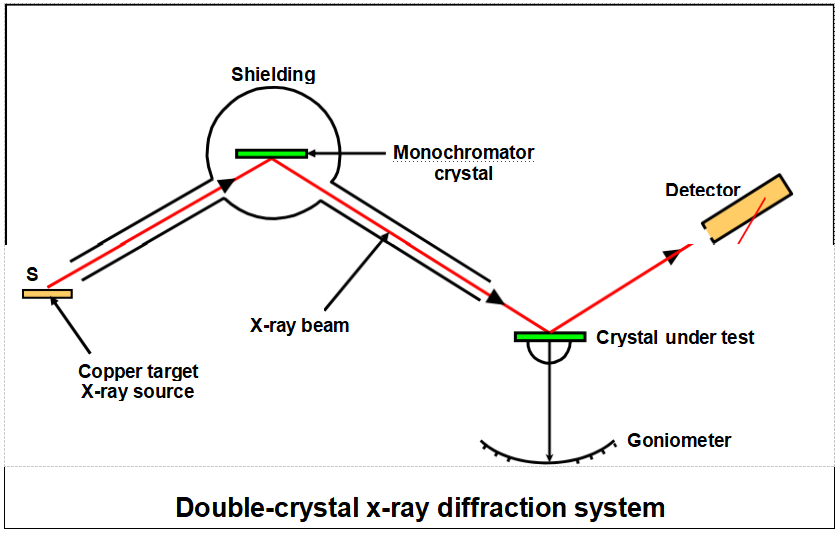
X-ray Orientation of Crystal Plates

Contamination Control

Contamination control is essential during the fabrication of resonators because contamination can adversely affect:

• Stability  (see  chapter  4)

-     aging

-     hysteresis

-     retrace

-     noise

-  nonlinearities and resistance anomalies ( high   starting

resistance , second - level   of   drive, intermodulation in filters)

-   frequency   jumps?

•  Manufacturing yields

•    Reliability

Crystal Enclosure Contamination

The enclosure and sealing process can have important influences on resonator stability.

 

•  A monolayer of adsorbed contamination contains ~ 1015 molecules/cm2 (on a smooth surface)

•  An enclosure at 10-7 torr contains ~109  gaseous molecules/cm3

 

Therefore:

In a 1 cm3 enclosure that has a monolayer of contamination

on its inside surfaces, there are ~106 times more adsorbed

molecules than gaseous molecules when the enclosure is sealed at 10-7 torr. The desorption and adsorption of such adsorbed

molecules leads to aging, hysteresis, retrace, noise, etc.

Milestones in Quartz Technology

1880      Piezoelectric effect discovered by Jacques and Pierre Curie

1905      First hydrothermal growth of quartz in a laboratory - by G. Spezia

1917      First application of piezoelectric effect, in sonar

1918      First use of piezoelectric crystal in an oscillator

1926      First quartz crystal controlled broadcast station

1927      First temperature compensated quartz cut discovered 1927

 First quartz crystal clock built

1934      First practical temp. compensated cut, the AT-cut, developed

1949     Contoured, high-Q, high stability AT-cuts developed

1956      First commercially grown cultured quartz available

1956      First TCXO described

1972      Miniature quartz tuning fork developed; quartz watches available

1974     The SC-cut (and TS/TTC-cut) predicted; verified in 1976

1982      First MCXO with dual c-mode self-temperature sensing

Quartz Resonators for Wristwatches

Requirements :

•     Small size

•     Low power dissipation (including the oscillator)

•     Low cost

 

•     High stability (temperature, aging, shock, attitude)

These requirements can be met with 32,768 Hz quartz tuning forks

Why 32,768 Hz?

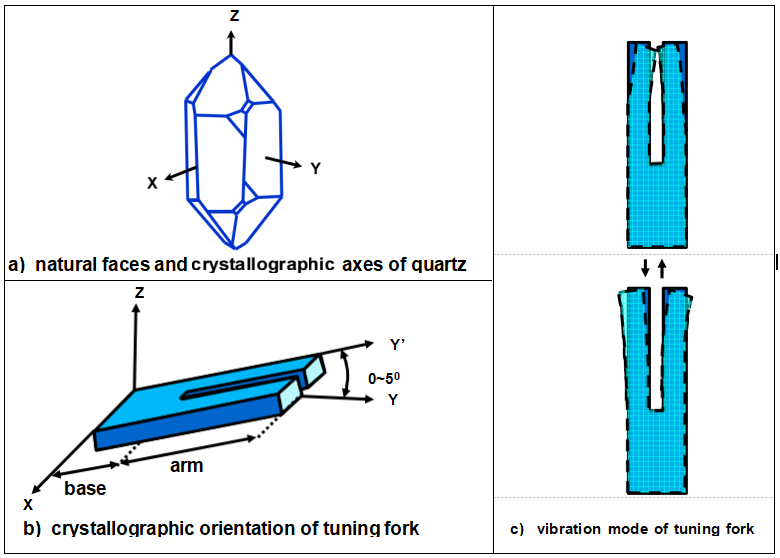
Quartz Tuning Fork

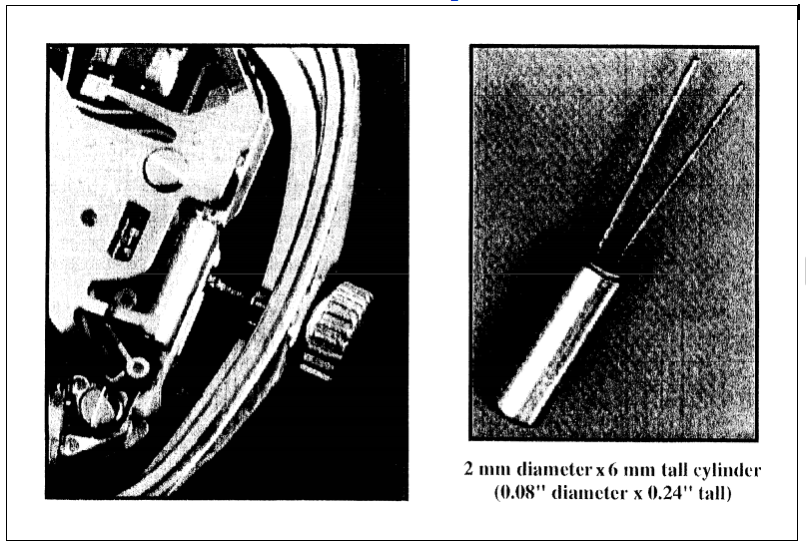
Watch Crystal

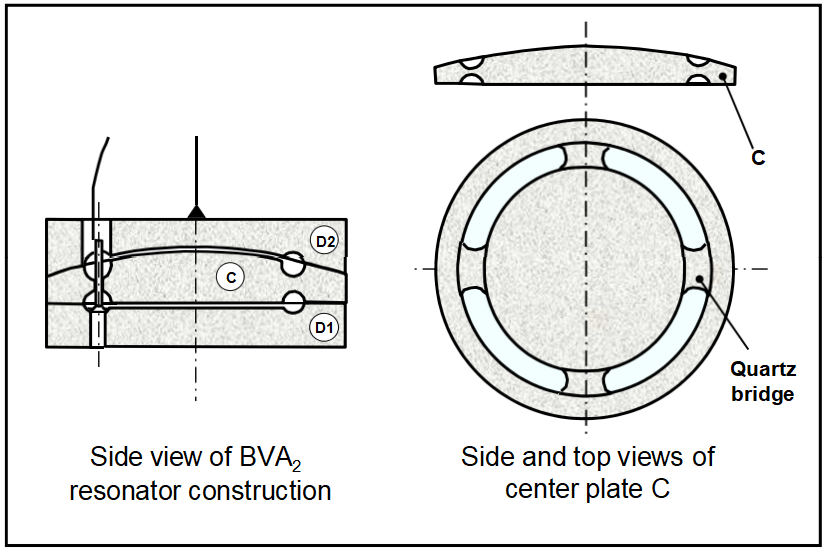
Electrodeless (BVA) Resonator

The Units of Stability in Perspective

• What is one part in 1010  ?  (As in 1 x 10-10/day aging.)

• ~1/2 cm out of the circumference of the earth.

• ~1/4 second per human lifetime (of ~80 years).

• Power received on earth from a GPS satellite, -160 dBW, is as  “bright” as a flashlight in Los Angeles would look in New York City, ~5000 km away (neglecting earth’s curvature).

• What is -170 dB?  (As in -170 dBc/Hz phase noise.)

• -170 dB = 1 part in 1017 ≈ thickness of a sheet  of paper out of the total distance traveled by all the cars in the world in a day.

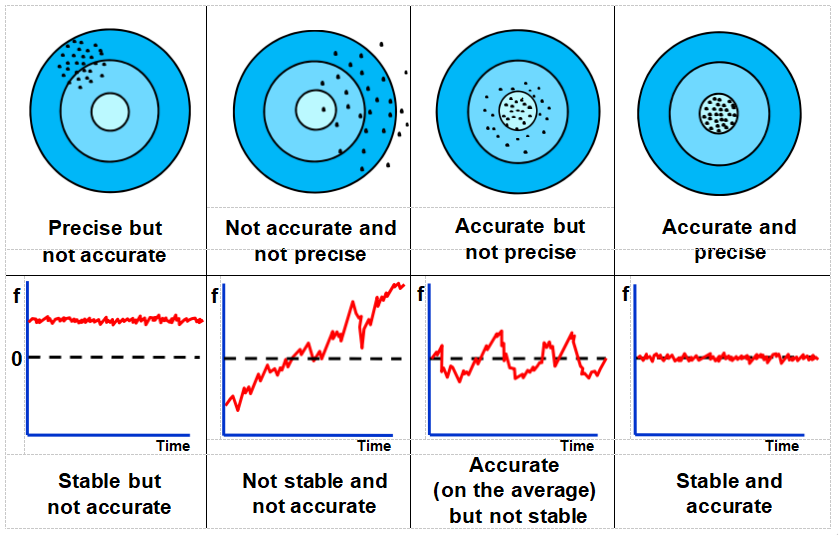
Accuracy, Precision, and Stability

Influences on Oscillator Frequency

Idealized Frequency-Time-Influence Behavior

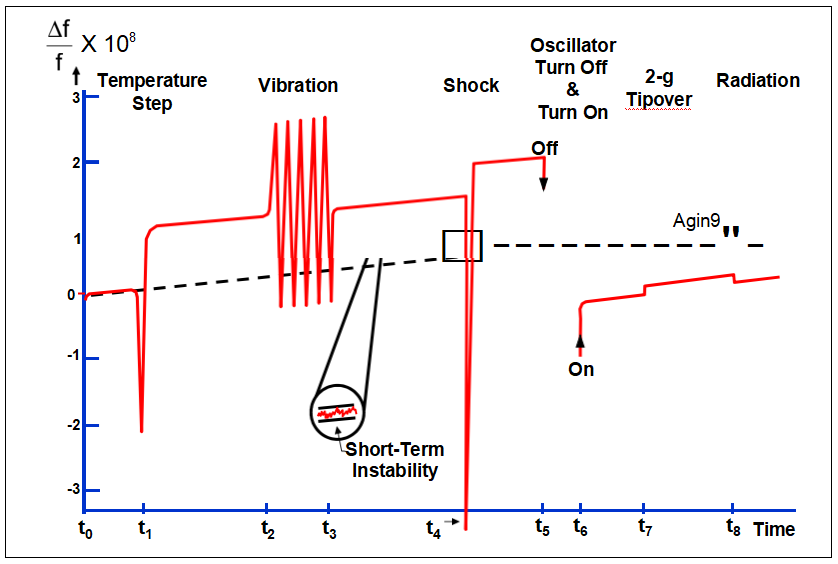
Aging and Short-Term Stability

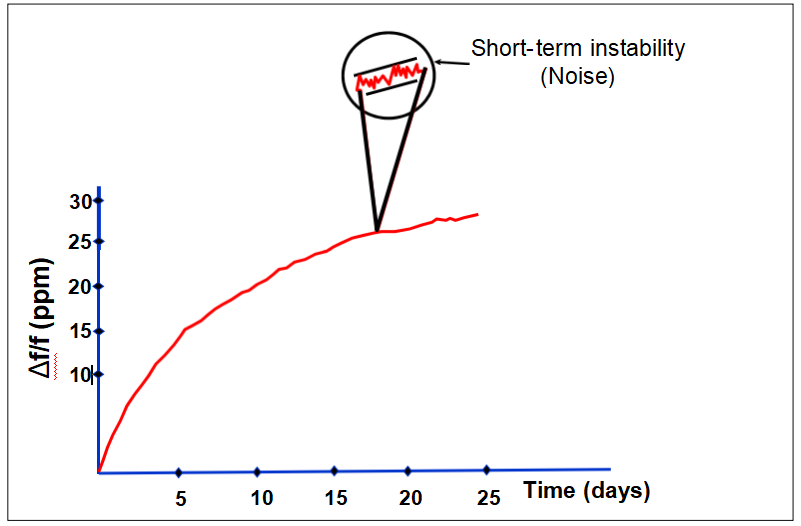
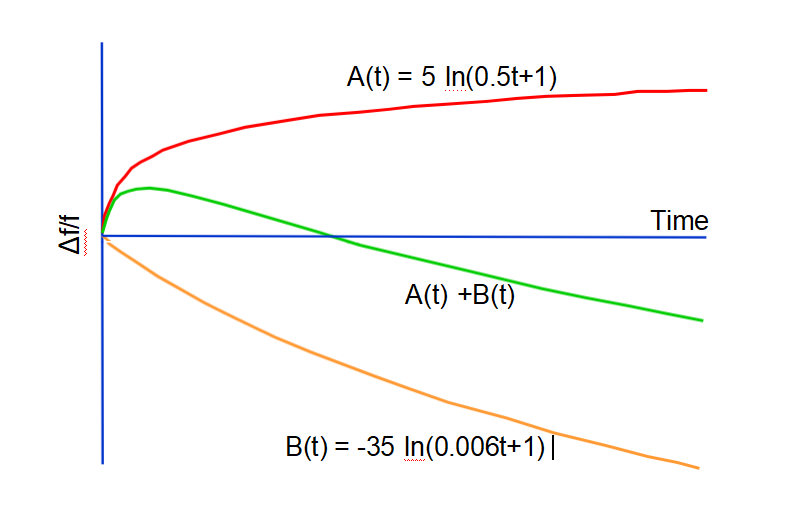
Aging Mechanisms

l  Mass   transfer   due   to   contamination

Since f ∝ 1/t, Δf/f = -Δt/t; e.g., f5MHz Fund ≈ 106 molecular layers, therefore, 1 quartz-equivalent monolayer ⇒ Δf/f ≈ 1 ppm

l  Stress   relief  in the resonator's: mounting and bonding structure, electrodes, and in the quartz (?) 

l Other effects

   Quartz outgassing

   Diffusion effects

   Chemical reaction effects

   Pressure changes in resonator enclosure (leaks and outgassing)

   Oscillator circuit aging (load reactance and drive level changes)

   Electric field changes (doubly rotated crystals only)

   Oven-control circuitry aging

Typical Aging Behaviors

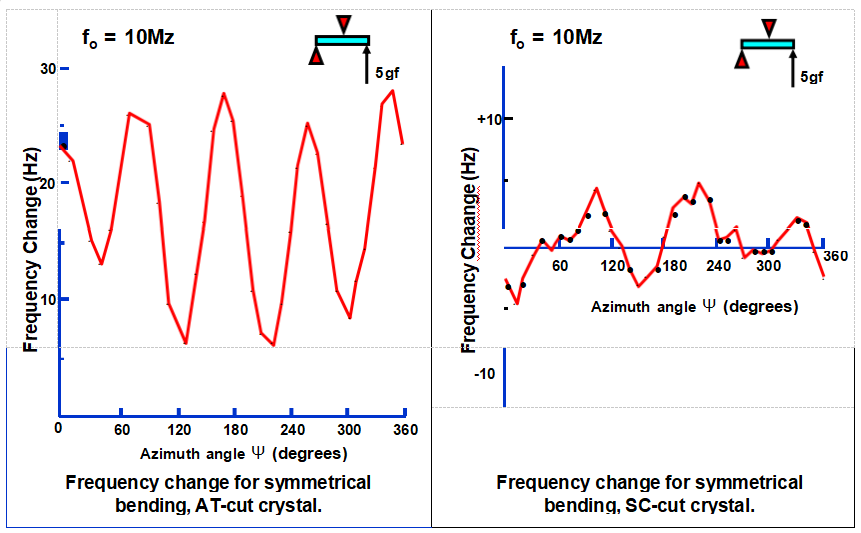
Stresses on a Quartz Resonator Plate

Causes :

•  Thermal expansion coefficient differences

•   Bonding materials changing dimensions upon solidifying/curing

•   Residual stresses due to clip forming and welding operations, sealing

•   Intrinsic stresses in electrodes

•   Nonuniform growth, impurities & other defects during quartz growing

•   Surface damage due to cutting, lapping and (mechanical) polishing

 

Effects :

•   In-plane diametric forces

•  Tangential (torsional) forces, especially in 3 and 4-point mounts

•   Bending (flexural) forces, e.g., due to clip misalignment and electrode stresses

•   Localized stresses in the quartz lattice due to dislocations, inclusions, other impurities, and surface damage

Bending Force vs. Frequency Change

AT-cut resonator                                 SC-cut resonator

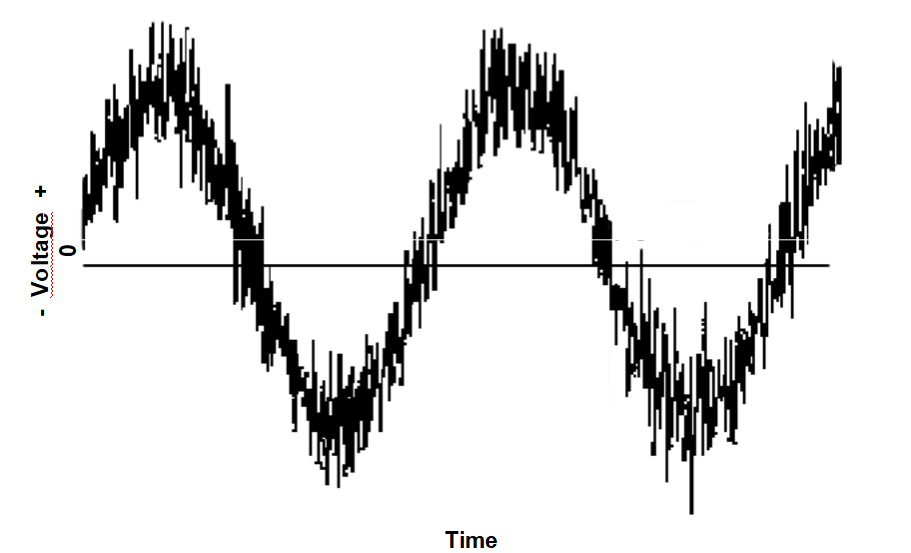
Short Term Instability (Noise)

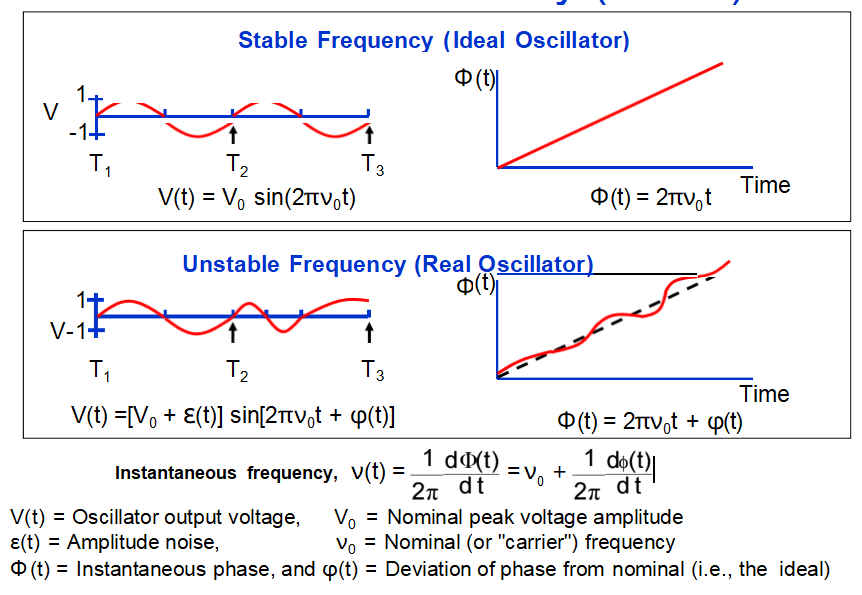
Instantaneous Output Voltage of an Oscillator

Impacts of Oscillator Noise

•     Limits the ability to determine the current state and the predictability of oscillators

•     Limits syntonization and synchronization accuracy

•     Limits receivers' useful dynamic range, channel spacing, and selectivity; can limit jamming resistance

•     Limits radar performance (especially Doppler radar's) •     Causes timing

 errors [~τσ y(τ )]

•     Causes bit errors in digital communication systems

•     Limits number of communication system users, as noise from transmitters interfere with receivers in nearby channels

•     Limits navigation accuracy

•     Limits ability to lock to narrow-linewidth resonances

•     Can cause loss of lock; can limit acquisition/reacquisition capability in phase-locked-loop systems

Time Domain - Frequency Domain