Tutorial on Frequency Control and Timing Application of Quartz Crystal Resonators and Oscillators (Part 5)

Sine Vibration-Induced Phase Noise

Sinusoidal vibration produces spectral lines at ±fv from the carrier, where fv is the vibration frequency.

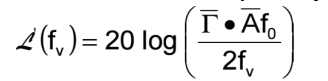
e.g., if  Γ   = 1 x 10 -9/g and f 0  = 10 MHz, then even if the

oscillator is completely noise free at rest, the phase  “noise”

i.e., the spectral lines, due solely to a sine vibration level of 1g will be;

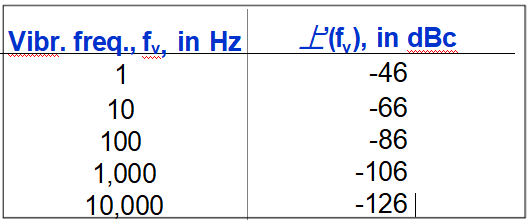
Random Vibration-Induced Phase Noise

Random vibration’s contribution to phase noise is given by:

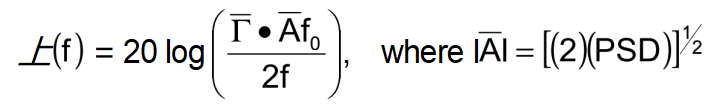
e.g., if  Γ   = 1 x 10 -9/g and f 0  = 10 MHz, then even if the

oscillator is completely noise free at rest, the phase  “noise”

i.e., the spectral lines, due solely to a vibration of power spectral density, PSD = 0.1 g2/Hz will be:

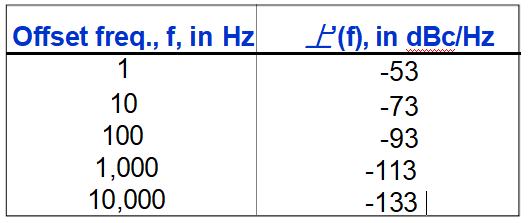
Random-Vibration-Induced Phase Noise

Phase noise under vibration is for Γ = 1 x 10-9  per g and f = 10 MHz

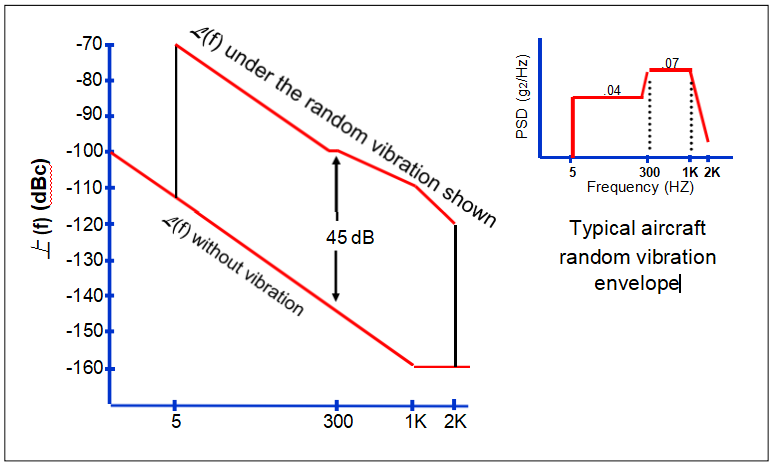
Acceleration Sensitivity vs. Vibration Frequency

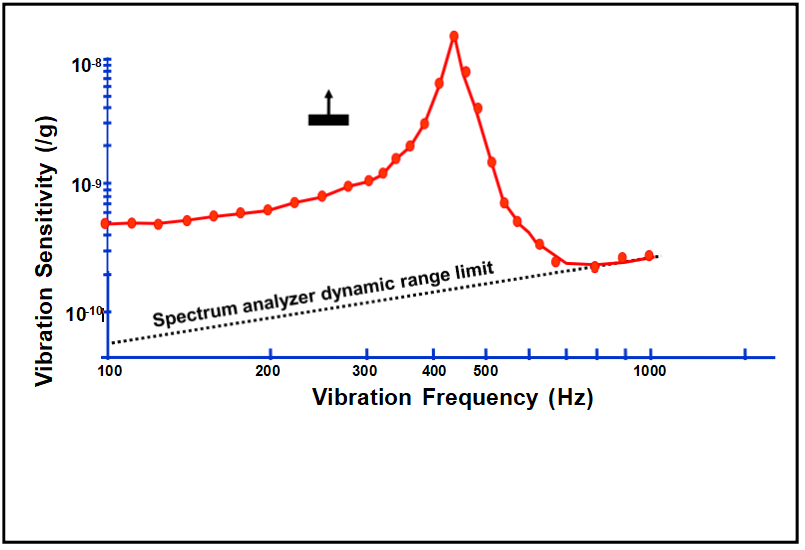
Acceleration Sensitivity of Quartz Resonators

    Resonator acceleration sensitivities range from the low parts in 1010  per g for the best commercially available SC-cuts, to parts in 107  per g for tuning-fork-type     watch crystals.  When a wide range of resonators were examined:  AT, BT, FC, IT,    SC, AK, and GT-cuts; 5 MHz 5th overtones to 500 MHz fundamental mode inverted mesa resonators; resonators made of natural quartz, cultured quartz, and swept

cultured quartz; numerous geometries and mounting configurations (including

rectangular AT-cuts); nearly all of the results were within a factor of three of 1x10-9 per g.  On the other hand, the fact that a few resonators have been found to have  sensitivities of less than 1x10-10  per g indicates that the observed acceleration

sensitivities are not due to any inherent natural limitations.

Theoretical and experimental evidence indicates that the major variables yet to be controlled properly are the mode shape and location (i.e., the amplitude of

vibration distribution), and the strain distribution associated with the mode of

vibration.  Theoretically, when the mounting is completely symmetrical with respect to the mode shape, the acceleration sensitivity can be zero, but tiny changes from  this ideal condition can cause a significant sensitivity. Until the acceleration

sensitivity  problem is solved, acceleration compensation and vibration isolation can provide lower than 1x10-10  per g, for a limited range of vibration frequencies, and at  a cost.

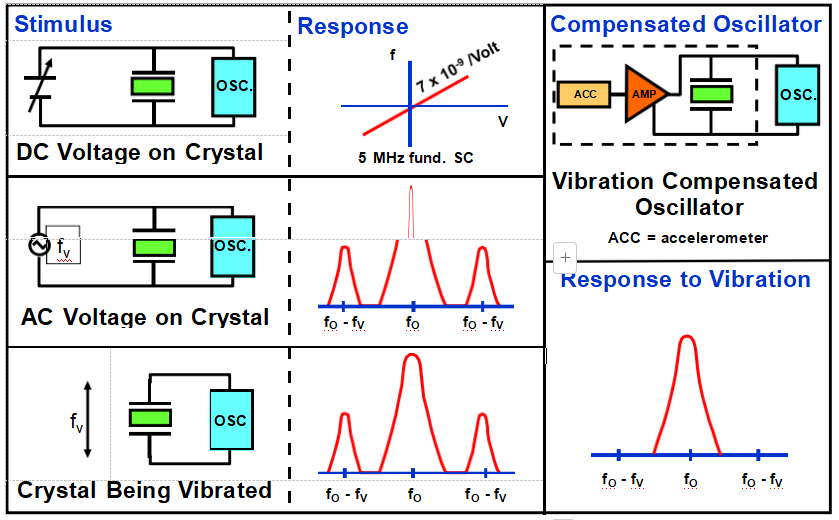
Vibration Compensation

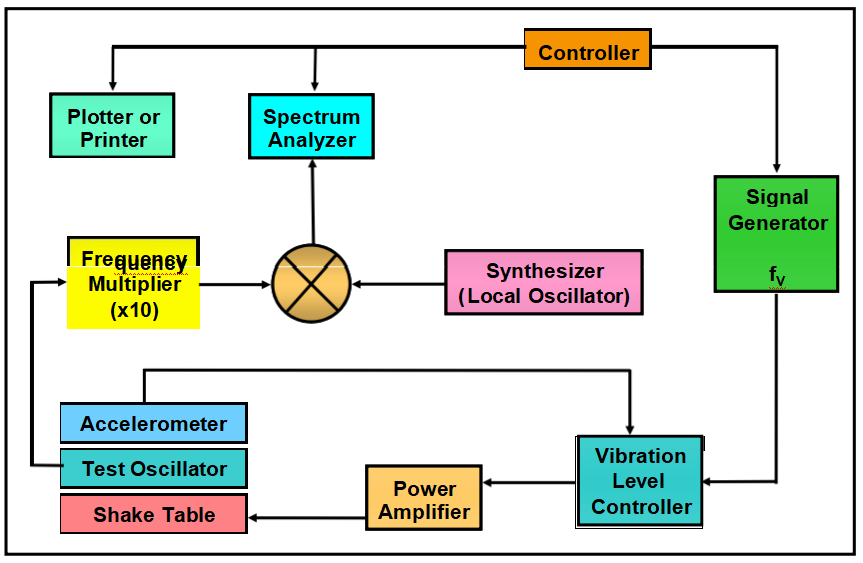
Vibration Sensitivity Measurement System

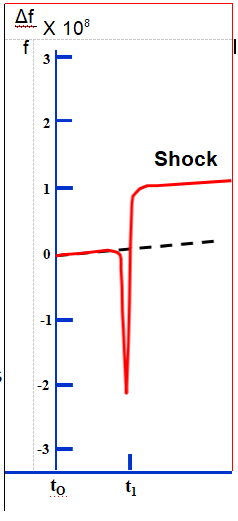
Shock

The frequency excursion during a shock is due to    the resonator’s stress sensitivity.  The magnitude of the excursion is a function of resonator design, and of the shock induced stresses on the resonator (resonances in the mounting structure will

amplify the stresses.)  The permanent frequency offset can be due t shock induced stress

changes, a change in (particulate) contamination on the resonator surfaces, and changes in the

oscillator circuitry.  Survival under shock is primarily a function of resonator surface imperfections.

Chemical-polishing-produced scratch-free resonators have survived shocks up to 36,000 g in air gun tests,  and have survived the shocks due to being fired from a 155 mm howitzer (16,000 g, 12 ms duration).

Other Effects on Stability

l Electric field -affects doubly-rotated resonators; e.g., a voltage on the electrodes of a 5 MHz fundamental mode SC-cut resonator results in a Δf/f = 7 x 10-9  per volt.  The voltage can also  cause sweeping, which can affect the frequency (of all cuts), even at normal operating

temperatures.

l Magnetic field -quartz is diamagnetic, however, magnetic fields can induce Eddy currents, and will affect magnetic materials in the resonator package and the oscillator circuitry.  Induced ac    voltages can affect  varactors, AGC circuits and power supplies. Typical frequency change of a  "good" quartz oscillator is <<10-10  per gauss.

l Ambient   pressure (altitude) -deformation of resonator and oscillator packages, and change in heat  transfer conditions affect the frequency.

l Humidity -can affect the oscillator circuitry, and the oscillator's thermal properties, e.g., moisture absorbed by organics can affect dielectric constants.

l Power supply voltage, and load   impedance   -  affect the oscillator circuitry, and indirectly, the   resonator's drive level and load reactance.  A change in load impedance changes the amplitude or phase of the signal reflected into the oscillator loop, which changes the phase (and

frequency) of the oscillation. The effects can be minimized by using a (low noise) voltage regulator and buffer amplifier.

l Gas permeation -  stability can be affected by excessive levels of atmospheric hydrogen and    helium diffusing into "hermetically sealed" metal and glass enclosures (e.g., hydrogen diffusion through nickel resonator enclosures, and helium diffusion through glass Rb standard bulbs).

Interactions Among Influences

In attempting to measure the effect of a single influence, one often encounters interfering influences, the presence of which may or may not be obvious.