Chapter 2: Operating Oscillation Margin and Excitation Power for Evaluating Oscillation Circuits (Oscillation Circuit Evaluation Method 2)

The equivalent impedance (Re) of a quartz crystal unit when connected to a load can be calculated using equation (2).

R1 is the equivalent series impedance of a quartz crystal unit without load capacitance.

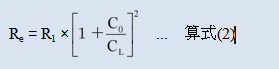
Using the quartz crystal unit constant (R1=33.7 Ω) introduced in the previous "Evaluation Method for Oscillating Circuits (1)" C0=1.11pF、CL=7.8pF），  After substituting the above equation (2), the equivalent impedance (Re) can be calculated to be 44 Ω.

At this point, R1 is the measured value of the quartz crystal unit, not the parameter value. Assuming the maximum value of R1 is 57 Ω, Re increases to 74 Ω due to the influence of the load capacitance, please note.

Figure 2 shows an example of inserting impedance to test negative impedance.

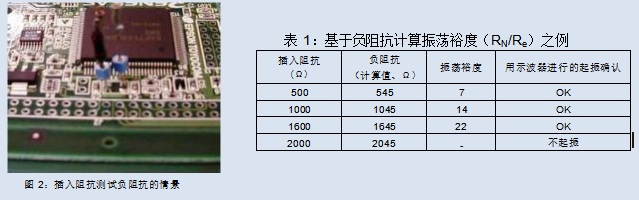
Confirm the waveform with an oscilloscope in the state shown in Figure 2. Gradually increase the inserted impedance value r and search for impedance points that do not vibrate. At this point, the decrease in oscillation output and the change in oscillation frequency caused by the insertion impedance are ignored, and only the determination of whether to start oscillation is made.

After determining the negative impedance RN, calculate the oscillation margin RN/Re (Table 1 above).

It should be noted that low oscillation margin will lead to various adverse phenomena, such as unstable oscillation, no oscillation or longer oscillation time caused by uneven circuit characteristics.

When the oscillation margin is more than 5 times, it means that the oscillation circuit has sufficient ability to excite quartz crystal units (amplification degree), and usually no problems will occur. If the oscillation margin is below 5 times, it is recommended to change the circuit constant of the oscillation circuit, increase the negative impedance RN, or reduce the equivalent series impedance Re of the quartz crystal unit to maintain the oscillation margin above 5 times.

Although reducing the circuit constant of oscillation circuits such as fine-tuning capacitors (Cg, Cd) or current limiting resistors (Rd) can increase the negative impedance and oscillation margin, it should be noted that the load capacitance of oscillation circuits changes with the circuit constant, which will also cause changes in oscillation frequency. To reduce the equivalent series resistance R1 of quartz crystal units, a request needs to be made to the quartz crystal manufacturer.

【2】 Evaluation of excitation power

Excitation power refers to the power consumed by quartz crystal units during oscillation. Usually, it is best to control the excitation power within the specifications of the quartz crystal unit, usually below about 100 μ W, but it should be noted that there are slight differences among quartz crystal manufacturers.

When the excitation power is too high, it will cause changes in the oscillation frequency, a decrease in stability, changes in equivalent circuit parameters, or frequency distortion. High excitation power may also lead to repeated abnormal oscillations and the consequences of faults. Calculate the excitation power (P) using the following equation (3).

P = I2 × Re         ...      Equation (3)

Here I is the current flowing through the quartz crystal unit, and Re is the equivalent resistance of the quartz crystal unit when loaded. If the excitation power exceeds the specification parameters, it is necessary to adjust the constant of the oscillation circuit to reduce the current flowing through the quartz crystal unit. Reducing Cg or Cd can reduce the excitation power, but the load capacitance of the oscillation circuit will also change accordingly. The simplest method is to increase Rd, but the loss will increase and the negative impedance will decrease accordingly.

The excitation power cannot be directly measured.

Place the test needle on the HOT terminal of the quartz crystal unit combined with the oscillation circuit, use an oscilloscope to test the applied voltage Vpp, and calculate the current flowing through the quartz crystal unit based on the measured value.

Figure 3 shows the scenario when testing the excitation power.

Insert the current probe into the terminal of the quartz crystal unit used for evaluation, and then install it into the quartz crystal unit of the printed circuit board. After confirming the oscillation through an oscilloscope, measure Vpp based on the waveform.

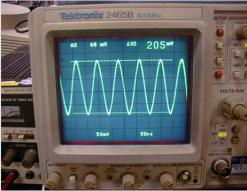
Figure 3: Scenario for testing excitation power

For example, assuming that Vpp=0.205V is obtained from the waveform of the oscilloscope, the testing probe is set to 1mA/div, the probe impedance is 50 Ω, the testing range of the oscilloscope is 50mV/div, and the equivalent resistance Re of the quartz crystal unit with load is 45 Ω, then

Vpp/50[mV/div]=205/50=4.1div 

4.1/（2 √2）=1.45div

50[mV/div]/50 Ω=1mA/div，

From this, it can be concluded that the current I flowing through the quartz crystal unit is 1.45 div x 1 mA/div=1.45 mA.

According to equation (3) on the previous page, the excitation power P is calculated to be 1.45 x 1.45 x 45=95 μ W.

【3】 End

We explained the evaluation method of oscillation circuits in two parts. To make the best oscillation circuit, it is necessary to consider (1) frequency matching, (2) oscillation margin (negative impedance), and

(3) Optimize the excitation power separately.

Although setting the optimal circuit constant for any of the above is the most ideal approach, there may also be situations where it is not suitable in practical work. We have summarized the response methods at the end.

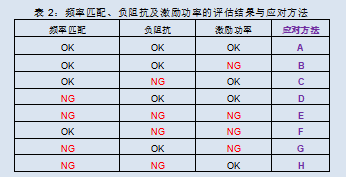
A. Use the circuit constant used for evaluation.

B. It is necessary to review the specifications and parameters of quartz crystal units related to excitation power. Please confirm whether the excitation power of this evaluation result affects the quartz crystal unit.

C. It is necessary to review the specifications and parameters of quartz crystal units related to negative impedance. Please consider changing the specification parameter R1 of the equivalent series impedance of the quartz crystal unit to achieve an oscillation margin of more than 5 times.

Regarding frequency matching, it is necessary to consider adjusting the pre specified standard load capacitance to the actual load capacitance of the substrate assembled with quartz crystal units.

E... It is necessary to adopt a combination of "B+C+D" as a response method.

F. It is necessary to adopt a combination of "B+C" as a response method.

G... It is necessary to adopt a combination of "B+D" as a response method.

H... It is necessary to adopt a combination of "C+D" as a response method.